Mass-spring-damper System

A mass-spring-damper MSD system is a discretized model of any dynamic system. In any case we assume that the resistive force is proportional to the speed dudtof. Mass-Spring-Damper in Simulink and Simscape. Spring elastic element Damper frictional element Mass inertia element Translational and rotational versions These are passive non-energy producing devices Driving Inputs force. The inertial effect of the dynamic system is related through this lumped mass. If the elastic limit of the spring is not exceeded and the mass hangs in equilibrium the spring will extend by an amount e such that by Hookes Law the tension in the. The damping coefficient c is simply defined as the damping force divided by shaft velocity.

Transfer function and state space model are developed for system shown below.

I Derive the equations of motion. Spring elastic element Damper frictional element Mass inertia element Translational and rotational versions These are passive non-energy producing devices Driving Inputs force. In this note MEscope is used to explore the properties of the mass-spring-damper system shown in the figure below. The spring friction between the mass and the guides if any that constrain its motion to one dimension or a mechanical device dashpot that imparts a resistive force to the mass. Mass-Pulley System A mechanical system with a rotating wheel of mass m w uniform mass distribution. Governing equation is same as in previous example ie based on Newtons second law.

Entropy Free Full Text Modeling Of A Mass Spring Damper System By Fractional Derivatives With And Without A Singular Kernel

Mass-spring-damper system. Write all the modeling equations for translational and rotational motion and. In this note MEscope is used to explore the properties of the mass-spring-damper system shown in the figure below. Next the nonlinear vibrations of a coupled 0core90 sandwich cylindrical shell and spring-mass-damper system is examined.

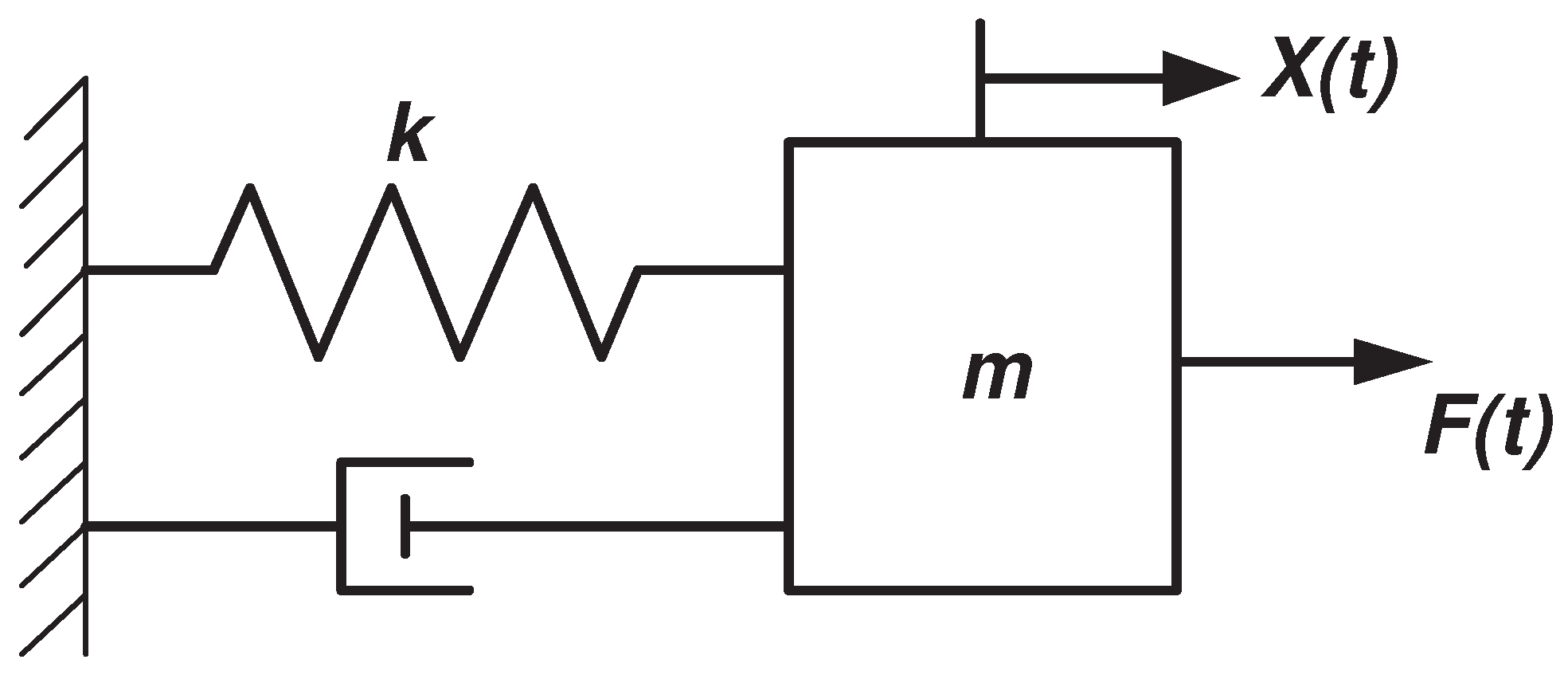
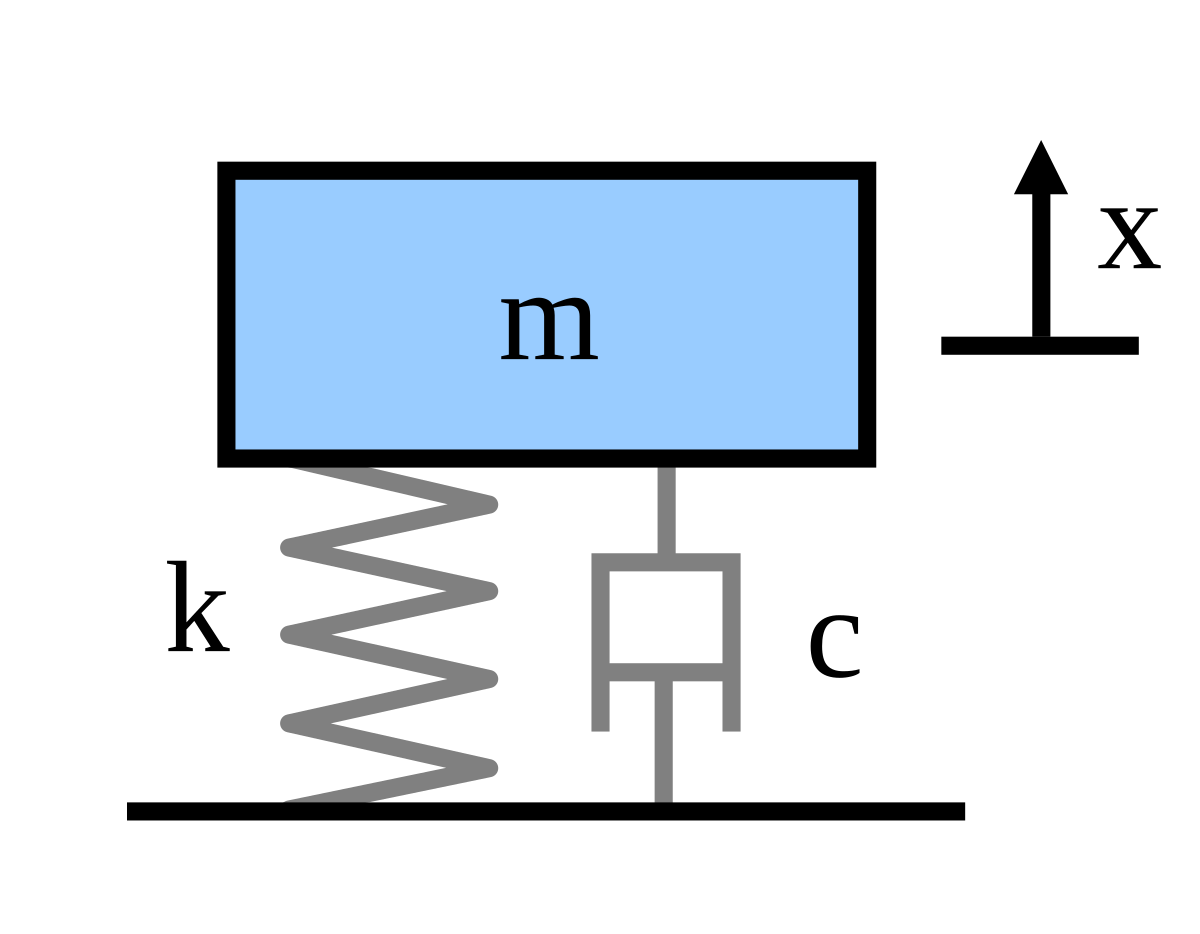
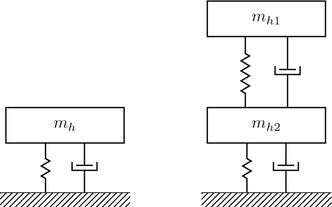
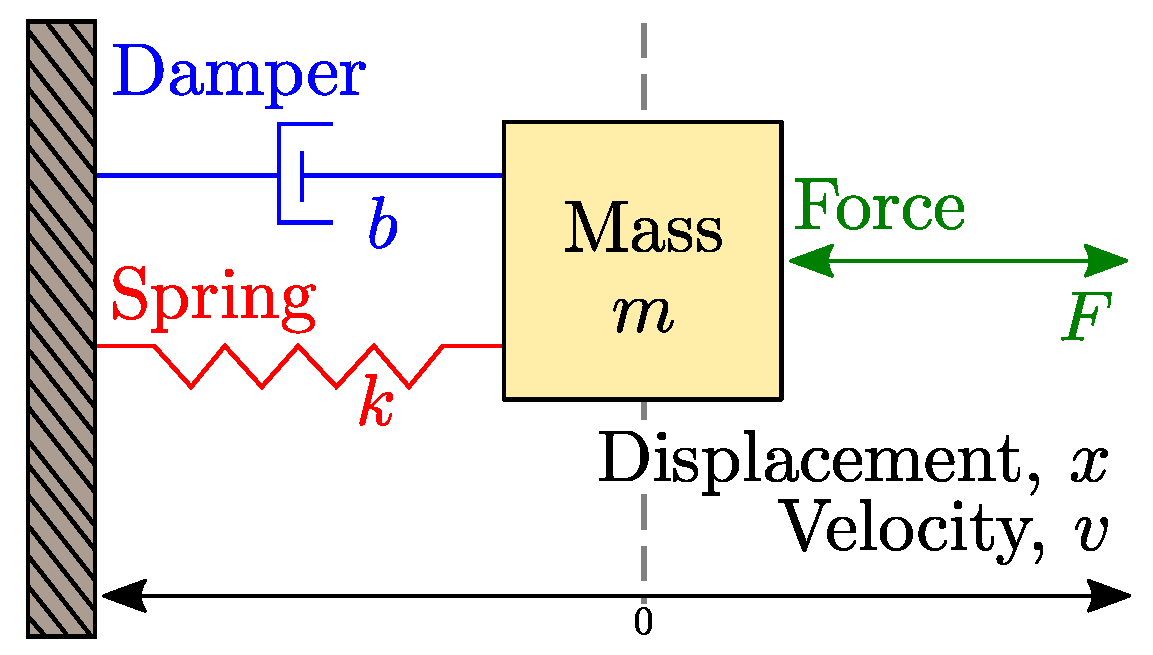
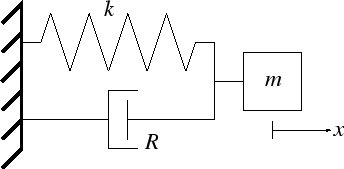
All systems possessing mass and elasticity are capable of free vibration or vibration that takes place in the absence of external excitation. The spring has stiffness k the damper has coefficient c the block has mass m and the position of the mass is measured by the variable x. Assume the springs are at rest no stretch or compression when dı d2 0.

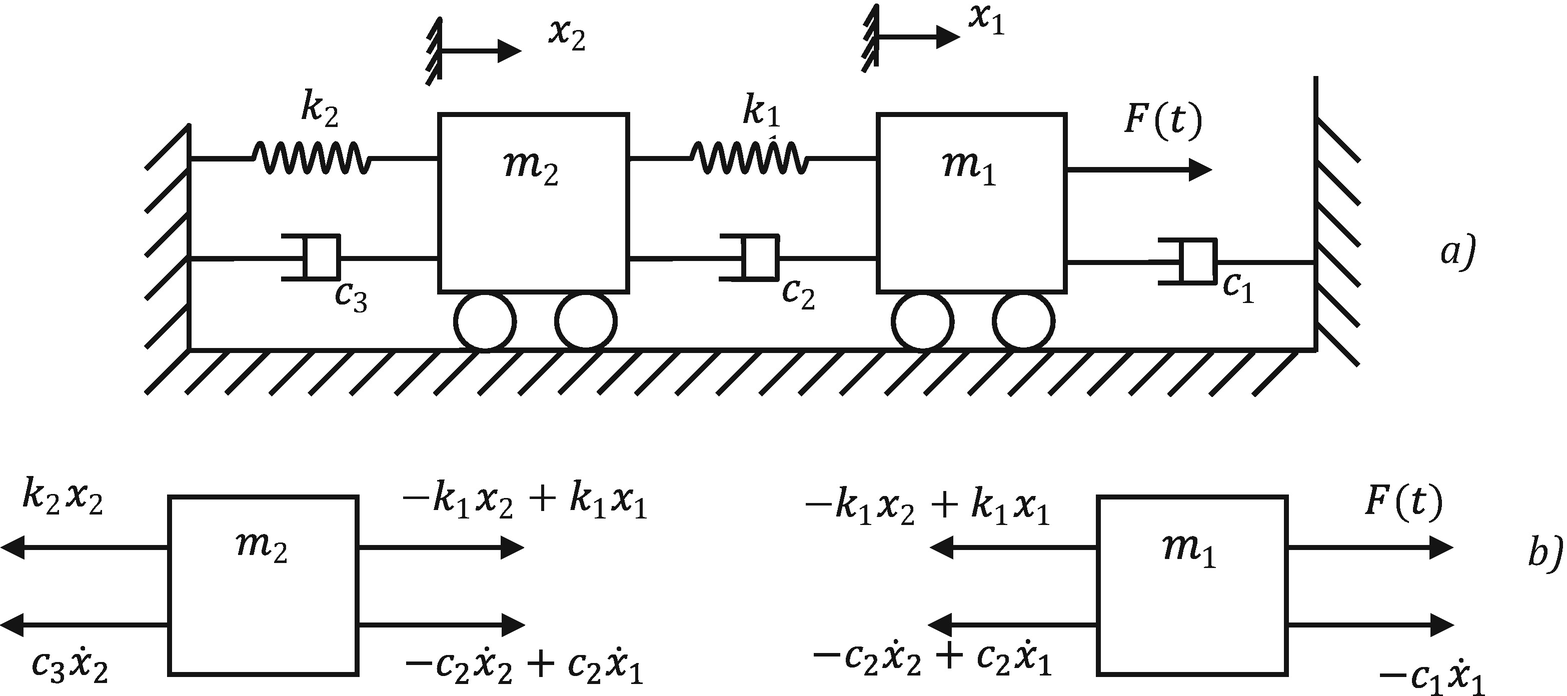
I Derive the equations of motion. Where m 025 slug c 2 lb-secft k 25 lbft and f t lb is the externally applied force shown in Figure P839The forcing function can be expanded in a Fourier series as follows. If the elastic limit of the spring is not exceeded and the mass hangs in equilibrium the spring will extend by an amount e such that by Hookes Law the tension in the.

PID Position Control of a Spring-Mass-Damper. Spring elastic element Damper frictional element Mass inertia element Translational and rotational versions These are passive non-energy producing devices Driving Inputs force. Of primary interest for such a system is its natural frequency of vibration.

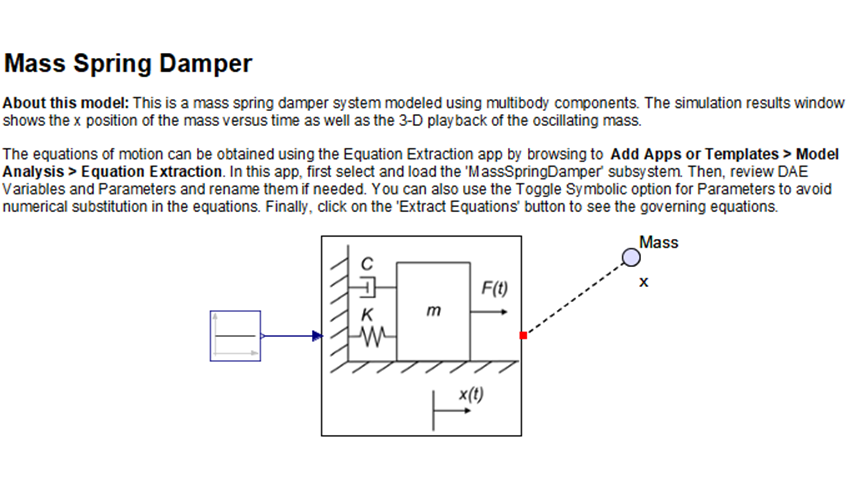
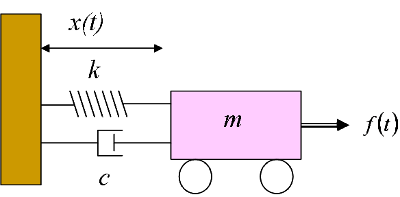
Transfer function and state space model are developed for system shown below. Output z t. A mass-spring-damper MSD system is a discretized model of any dynamic system.

L 2 m R 05 m middle radius H 0015The face sheets and the core layer are of the same thickness. Its equation of motion will be solved for its mode of vibration. Mass-spring systems are second order linear differential equations that have variety of applications in science and engineering.

The transfer function of the SMD with the actuating force F a. Then an FRF will be synthesized using its mode shape and its stiffness and mass lines will be examined.

Dsc Mass Spring Damper Concept Youtube

Spring Mass Damper System 1dof Youtube

301 Vibration Of Mass Spring Damper System Memorandums Of A Novice Automotive Engineer

A Simple Mass Spring Damper System Download Scientific Diagram

Mass Spring Damper Model Wikipedia

Mass Spring Damper System

Robust Tuning Of Mass Spring Damper System Matlab Simulink Mathworks Benelux

File Mass Spring Damper Png Wikimedia Commons

File Mass Spring Damper System Critically Damped Gif Wikimedia Commons

Solving A System Of Mass Spring Damper And Coulomb Friction Stack Overflow

Mass Spring Damper System For An Example Modeling Problem Download Scientific Diagram

Mechanical Vibrations 8 Newton 2 Double Mass Spring Damper System Youtube

Modeling A Mass Spring Damper System Physics Forums

Github Mathworks Teaching Resources Mass Spring Damper Systems Interactive Courseware Module That Addresses The Fundamentals Of Mass Spring Damper Systems Taught In Mechanical Engineering Courses

File Mass Spring Damper System Underdamped Gif Wikimedia Commons

Free Vibrations Of A Spring Mass Damper System Wolfram Demonstrations Project

Control Of A Spring Mass Damper System Using Mixed Mu Synthesis Matlab Simulink Example Mathworks America Latina

102 Matlab Analysis Of The Mass Spring Damper System Memorandums Of A Novice Automotive Engineer

Equation Generation Mass Spring Damper Multibody Multi Domain Physical Model In Maplesim Maplesoft

Comparing Closed Loop Control Models And Mass Spring Damper Models For Human Structure Interaction Problems Springerlink

General 2 Dof Mass Spring Damper System Download Scientific Diagram

Position Tracking Control Of Mass Spring Damper System With Time Varying Coefficients Semantic Scholar

Tuned Mass Spring Damper Design Application Center

1

Mass Spring Damper Draw Claytex

Symmetry Free Full Text Entropy Generation In A Mass Spring Damper System Using A Conformable Model

Spring Mass Damper Systems Springerlink

File Mass Spring Damper 2 Body System Svg Wikimedia Commons

302 Vibration Of Mass Spring Damper System 2 Memorandums Of A Novice Automotive Engineer

Latex Tutorial Easy Way To Make A Mass Spring Damper System Using Circuitikz Link To Code Below Youtube

Matlab Tutorial Simulation Of A Mass Spring Damper System

Solved 1 Consider The Mass Spring Damper System Shown In Chegg Com

Modeling And Experimentation Mass Spring Damper System Dynamics Pdf Free Download

The Nominal Two Masses Spring Damper System Download Scientific Diagram

State Space Representation Of A Mass Spring Damper System The Robotics Lab

Analysis Of Coupled Mass Spring Damper System By Changing Spring Constant Mass And Force Semantic Scholar

Restackor Spring Mass Damper Theory

Mass Spring Damper System Dynamics Dademuchconnection

Vibrating Systems

1 9 The Mass Damper Spring System A 2nd Order Lti System And Ode Engineering Libretexts

Solved We Modeled A Mass Spring Damper System During The Chegg Com

Compute The Damping Value For Two Masses In A Harmonic Oscillator Physics Stack Exchange

Mass Spring Damper Oscillator Simulation Example Enterprise Architect User Guide

Mass Spring Damper System 3d Cad Model Library Grabcad

Mech550f Multivariable Feedback Control Mass Spring Damper

Control Design Of Damper Mass Spring System Based On Backstepping Controller Scheme In International Review Of Applied Sciences And Engineering Volume 11 Issue 2 2020

Mass Spring Damper System

Initialize Variables For A Mass Spring Damper System Matlab Simulink Mathworks Espana

1

The geometrical dimensions of the shell are.

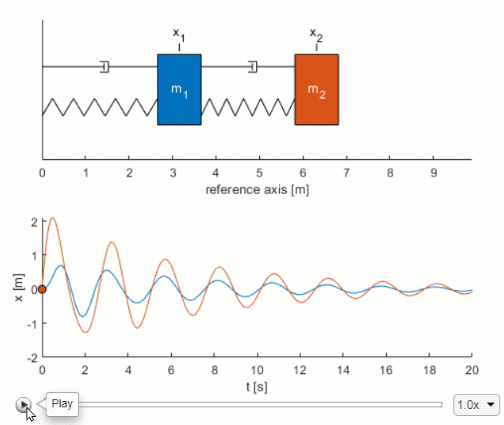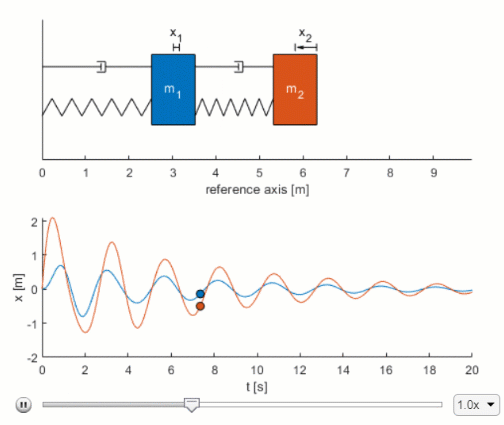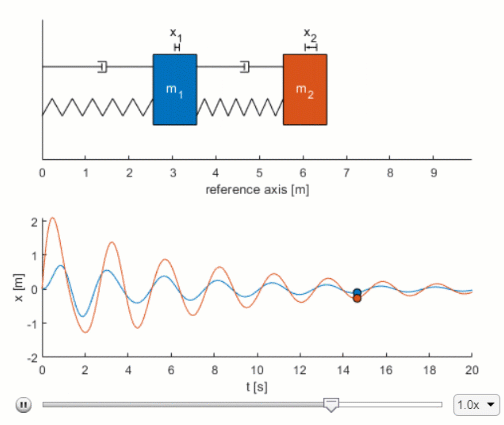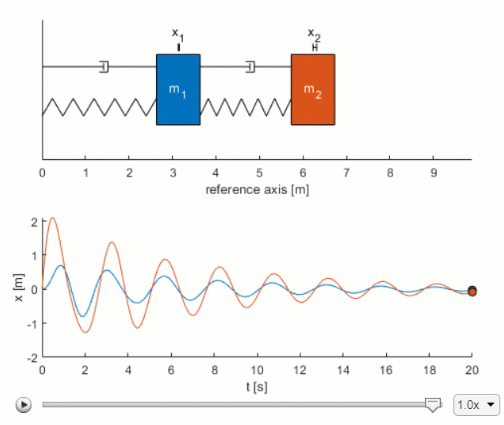
All systems possessing mass and elasticity are capable of free vibration or vibration that takes place in the absence of external excitation. Springs and dampers are connected to wheel using a flexible cable without skip on wheel. Spring elastic element Damper frictional element Mass inertia element Translational and rotational versions These are passive non-energy producing devices Driving Inputs force. From the results obtained it is clear that one of the systems was mass-damper-spring while the other was mass-nondamper-spring. Of primary interest for such a system is its natural frequency of vibration. The geometrical dimensions of the shell are. Write all the modeling equations for translational and rotational motion and. Difi d212 mi m2 1 C2 dį and d2 are the displacement of the carts and fi and f2 are the external forces applied to them. This example shows two models of a mass-spring-damper one using Simulink inputoutput blocks and one using Simscape physical networks.

In addition an external force P t is applied to the block and the displacement of the block is measured from the inertially. Mass-spring systems are second order linear differential equations that have variety of applications in science and engineering. Mass-Spring-Damper Systems The Theory The Unforced Mass-Spring System The diagram shows a mass M suspended from a spring of natural length l and modulus of elasticity λ. Of primary interest for such a system is its natural frequency of vibration. Demonstrates how to use the Mass Spring Damper System Simulation. Then the FRF will be curve fit to extract its modal parameters. Ii Put the equations of motion into standard state.